A mathematical model is developed by researchers from Vrije Universiteit Brussels and TU Eindhoven to calculate the costs of alternative distribution set-ups for last mile transportation in a FMCG supply chain with small and fragmented volumes. The model is based on input from logistics cost models for urban areas combined with cost variables related to logistics processes, receiver attributes and local city characteristics.
The cost variables for each aspect (logistics, receiver, city) influence the cost-effectiveness and applicability of an alternative distribution set-up. The model is applied on the delivery of fast moving consumer goods (FMCG) towards small independent retailers in a megacity. The current supply of these stores is characterized by high costs, inefficiency and unsustainability.
Distribution set-ups
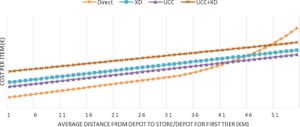
Four different set-ups are modelled. The case study focuses on an area within the megacity that is supplied from one distributor branch. It thus concerns the very last mile. In addition to the direct distribution set-up, three other set-ups leading to multi-echelon settings are modelled. In the second set-up, an additional cross-dock (XD) depot is added. In the XD goods are transshipped into smaller vehicles. No inventory is held at the cross-dock depots. The purpose of this set-up is to create more efficient transport by increasing vehicle fill rates. The third set-up concerns sharing a cross-dock depot and vehicles for final deliveries with other distributors in a UCC. The purpose is to increase the volume per vehicle by cooperating with other companies thereby decreasing the costs per item. In the final set-up goods are first shipped to a UCC and hereafter to a XD in order to decrease distances to the stores. Consequently this leads to a multi-echelon setting with three tiers.
The model shows the effects of different city and store request parameters. When drop sizes are low and distances are short, direct shipments with smaller vehicles outperform the current direct set-up. When drop sizes are low and distances are long, collaborating in an urban consolidation centre (UCC) shows a saving. The model can be further validated with data from other cities and other distribution set-ups.
To see the full paper, click here.